A tutto plasma! – Parte I

Una delle ricerche più promettenti per lo sviluppo di nuovi sistemi di propulsione spaziale è quella riguardo i propulsori al plasma.
L’obiettivo dei propulsori al plasma è lo stesso dei propulsori chimici convenzionali: espellere gas ad alta velocità per ottenere spinta nella direzione opposta.

In genere è convinzione comune che i razzi funzionino perché i gas espulsi “impattano” con oggetti e gas circostanti dell’atmosfera generando una spinta utile. Questa convinzione non è solo fallace, ma totalmente incoerente dato che i propulsori funzionano anche nello spazio (vuoto) e meglio rispetto che in atmosfera!!
Quindi prima di addentrarci nel mondo dei propulsori al plasma (progettati per operare nello spazio), capiamo meglio da un punto di vista fisico il meccanismo che permette ad un qualsiasi veicolo di muoversi.

Introduzione

Riuscire a spostarsi significa riuscire ad esercitare una forza (F) su “qualcosa” per un arco di tempo che va dall’istante da cui è cominciata l’azione (t₀) all’istante cui l’azione è terminata (t₁).
Per camminare sfruttiamo la forza d’attrito per spingere il suolo nella direzione opposta a dove vogliamo andare (III principio).
Ciò identifica la variazione della quantità di moto (Δp), ovvero la differenza fra la quantità di moto che il corpo aveva nell’istante in cui comincia la spinta (p(t₀)) e l’istante in cui la spinta si arresta (p(t₁)). E’ chiamata Impulso della forza (I). Compreso concettualmente il fenomeno che osserviamo e viviamo, possiamo provare a scriverlo in formule:

F*(t₁-t₀) = Δp
Δp = I = p(t₁) – p(t₀)

Questione di quantità di moto

Cos’è la quantità di moto? In cosa ne facciamo esperienza?
Si tratta di una grandezza fisica (p) descritta come il prodotto fra la massa di un corpo che si muove e la sua velocità. Ha sia un’intensità che una direzione. Perciò è definita vettoriale, e si conserva durante il moto.
Ne facciamo esperienza sempre e si conserva nel moto anche durante gli urti al contrario dell’energia cinetica che può provocare altri fenomeni. Motivo per cui ci è molto utile per descrivere i moti.

Parte dell’energia cinetica può ad esempio compiere lavoro deformando i corpi, disperdersi attraverso il calore prodotto dallo sfregamento fra le parti, e persino disperdersi come onde acustiche.
Quindi da quanto abbiamo visto riuscire a produrre un moto significa scambiare una variazione di quantità di moto fra due enti fisici regolato dal III principio della dinamica.

L’Esempio del Camminare

Riprendendo l’esempio del camminare, per renderci conto che anche noi “spostiamo” il suolo quando vogliamo muoverci in una direzione.
Immaginiamo che tutti gli esseri umani siano sull’equatore, e che si mettano a camminare ad una velocità di 1 metro al secondo in senso orario. Ovvero nel verso opposto alla rotazione terrestre, dunque da est ad ovest.Tutti eserciterebbero una forza spingendo il suolo (la Terra) indietro, ottenendo di conseguenza una spinta in avanti come reazione da parte della Terra. Se queste parole sembreranno strane, basterà rifletterci mentre camminiamo, ponendo attenzione al fenomeno che stiamo vivendo.
La variazione nella velocità di rotazione della terra sul proprio asse sarebbe nell’ordine dei 2*10^-13 metri al secondo. Significa che diminuirebbe di un contributo nell’ordine dei 2 decimi di picometro al secondo.

Dalla Quantità di Moto si ottiene la Propulsione

Dunque quanto visto si applica alla propulsione dei velivoli, dei natanti, ed ai razzi, anche se sembra meno intuitivo.
L’elica di un natante spinge l’acqua dietro alla nave, ottenendo una spinta in avanti.
Gli esoreattori di un aereo (ad esempio i turbogetti di un aereo di linea), spingono l’aria dietro l’aereo, ottenendo una spinta in avanti.Nella propulsione di un razzo manca un aspetto fondamentale che osserviamo per tutti gli altri esempi sopra elencati, ovvero la mancanza di un ente fisico ambientale, qualcosa di esterno al razzo su cui “spingere” per ottenere una “spinta uguale in intensità e verso contrario“.

Quindi anche la variazione della quantità di moto risponde sempre al terzo principio della dinamica, e per comprendere meglio ciò faremo uso dell’esempio del cannone.

Esempio del Cannone

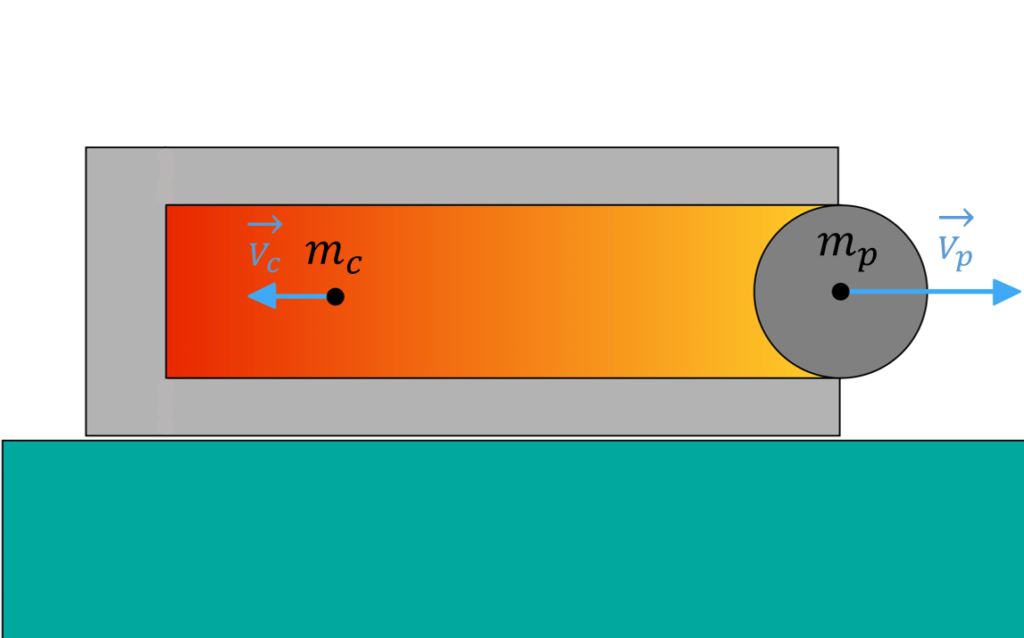
Attraverso l’esempio di un cannone possiamo intuire concettualmente il funzionamento di un propulsore per razzi.
Un cannone quando spara un proiettile è soggetto ad una forza uguale e contraria a quella che ha spinto il proiettile fuori dal cannone ad alta velocità. Si manifesta attraverso il fenomeno chiamato in gergo “rinculo”.
La forza con cui sia il proiettile sia il cannone sono spinti è la stessa (per il III principio). Però le accelerazioni cui sono soggetti sono diverse.
Ciò dipende dalla massa del proiettile (M_p) e dalla massa del cannone (M_c). La massa del primo è molto più piccola della massa del secondo (M_p << M_c).

Queste accelerazioni agiscono per l’intervallo di tempo dell’azione (t₁-t₀) fornendo una velocità al proiettile ed una velocità di rinculo al cannone.
Ogni volta osserviamo un moto ci rendiamo conto di una cosa interessantissima: la variazione della quantità di moto di un sistema è sempre pari a zero.
Nell’esempio, l’intensità della variazione della quantità di moto acquisita dal cannone (Δp₁) e quella del proiettile (Δp₂) sono le stesse, ma il loro verso è l’opposto poiché agiscono in versi opposti:

Δp₁ = -Δp₂
quindi, la variazione totale di quantità di moto del sistema cannone-proiettile è pari a zero:
Δp₁+Δp₂ = 0

Se così non fosse avremmo una “creazione di energia dal nulla”. Vedremo più in seguito che ciò sembra non valere in alcuni sistemi di propulsione ancora sotto studio, che sembrano essere dei sistemi detti “reactionless” ovvero che sembrano funzionare non rispettando apparentemente il III principio della dinamica. Qui di seguito un approfondimento:

Attraverso quanto visto, si può riuscire a capire concettualmente il funzionamento di un propulsore, seppur in maniera molto semplificativa.
Un propulsore non spara palle di cannone ma particelle di un gas. Nonostante siano molto piccole e siano dotate di una massa molto piccola il loro effetto non diviene più trascurabile quando sono tantissime!

Il “rinculo” del cannone equivale concettualmente alla spinta fornita dal propulsore. Le particelle devono uscire dal propulsore con una velocità molto elevata finché la spinta del razzo sia considerevole. Nei propulsori chimici è data dall’energia rilasciata dalla combustione che genera una vera e propria esplosione controllata. Perciò i propulsori che impieghiamo per lanciare i razzi nello spazio e che operano nello spazio non spingono su nulla di esterno al velivolo. Bensì spingono sulla materia che il velivolo si porta con sè e spinge fuori da sè quando deve variare la sua velocità.

L’Impulso Specifico Ponderale [I_sp] 

Nel far ciò, i propulsori sono classificati in funzione del loro Impulso Specifico Ponderale.
L’Impulso Specifico Ponderale (I_sp) è una grandezza che nasce dal rapporto fra l’Impulso fornito dal Propulsore e la forza peso del propellente espulso.
La sua unità di misura è il secondo [s].
Più questo valore è grande e meno combustibile il propulsore dovrà consumare a parità di spinta prodotta.
Alcuni esempi di I_sp di alcuni propulsori chimici:
I propulsori F-1 del Saturn V  avevano un I_sp = 263 s (al lancio).
I propulsori Merlin 1D del Falcon9 v1.1 hanno un I_sp = 282 s (al lancio).
Vedremo che i propulsori al plasma hanno un I_sp molto più elevato (da 1000 s a 10000s).

Definizione ed un po’ di Storia

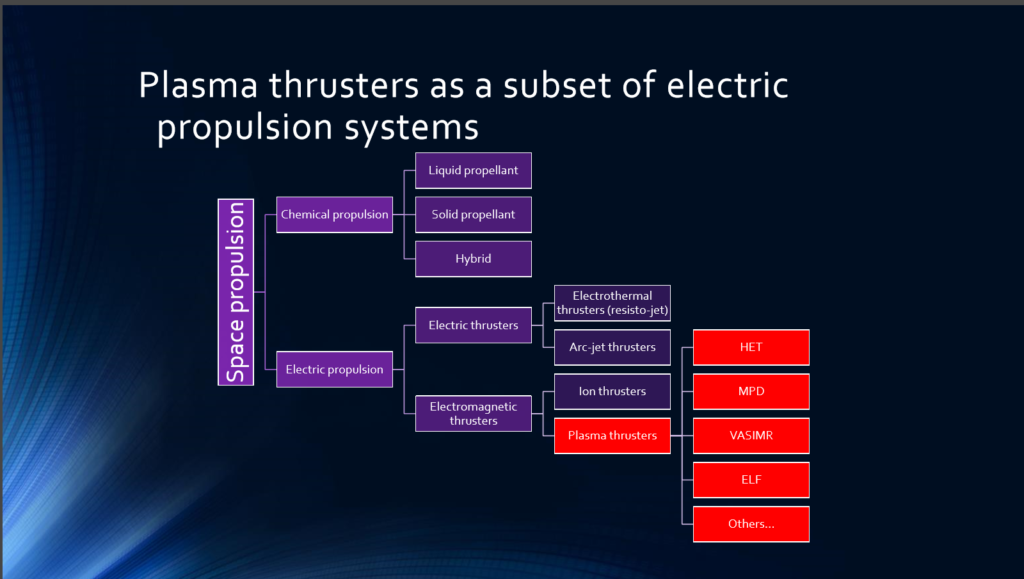
Entrambi i propulsori al plasma ed i propulsori ionici sono dei propulsori elettrici.
I propulsori al plasma si differenziano dai propulsori ionici per il meccanismo d’accelerazione, che nei primi è elettrodinamico e nei secondi elettrostatico.
Ci sono vari modi per ionizzare un gas rendendolo plasma e sviluppare delle interazioni elettrodinamiche tali da accelerarlo, ed a seconda del modo si classificano le tipologie di propulsori.

L’energia cinetica che forniscono all’astronave su cui sono montati deriva dall’energia prodotta dai generatori elettrici di bordo.
Infatti costituisce un gran vantaggio rispetto ai propulsori chimici perché la spinta non deriva dall’energia immagazzinata nel propellente ma dall’energia erogata dai generatori di potenza a bordo. Nonostante ciò, di contro presenta il seguente problema: finché si abbiano grandi spinte è necessario avere grandi potenze, e quindi bisogna utilizzare impianti in grado di erogare quantitativi di energia enormi che in parte ancora non abbiamo realizzato per l’impiego spaziale.

La possibilità di realizzare una propulsione elettrica in campo spaziale risale agli inizi del ‘900, da parte del fisico russo Kostantin Ciolkovskij.
I primi sviluppi risalgono agli inizi degli anni ’30 ma è solo verso la fine degli anni ’50, dopo il lancio del primo satellite artificiale Sputnik, che ci furono degli studi più intensi sia un URSS che USA.

La prima sonda dotata di Propulsori al Plasma fu la sonda Zond 2 decollata il 30 Novembre 1964 da Baikonur era dotata di 6 Pulsed Plasma Thrusters per orientare la navicella e modificarne la traiettoria.

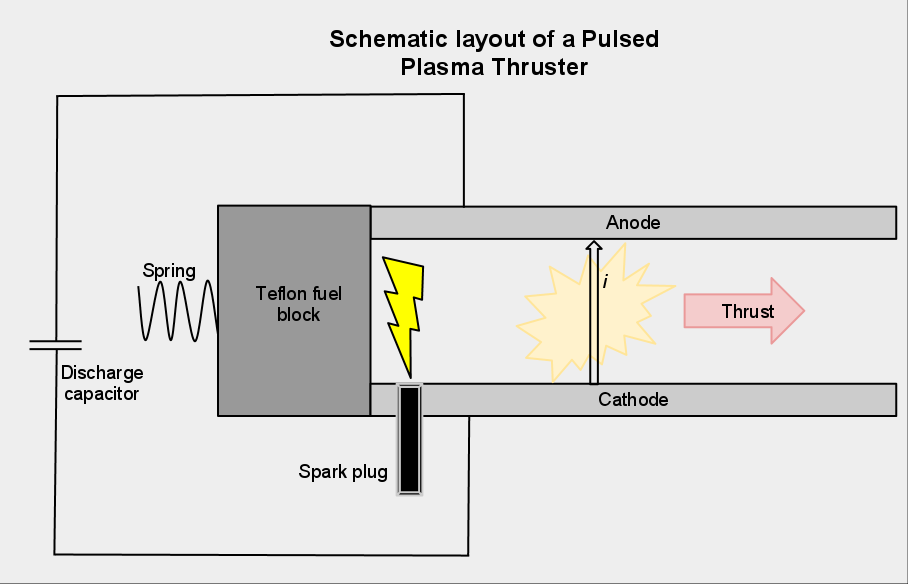
I Propulsori ad Impulsi di Plasma (PPT)

Sono dei propulsori composti da due piastre rettangolari funzionanti da elettrodi a cui viene applicata una differenza di potenziale nell’ordine dei kV. Il gas viene immesso fra gli elettrodi già ionizzato. Chiudendo il circuito fra le due piastre, genera una intensa corrente elettrica (I) che induce un inteso campo magnetico che attraverso la forza di Lorentz è in grado di accelerare il plasma lungo gli elettrodi, espellendolo ad alta velocità. Tale sistema è simile ad una “railgun”, un tipo di pistola elettromagnetica.

Nella Parte II e Parte III vedremo altre tipologie di propulsori come i Propulsori ad Effetto Hall (Hall Effect Thrusters, HET), i Propulsori MagnetoPlasmaDinamici (MagnetoPlasmaDynamic Thrusters, MPDT), ed il VASIMR.

Link:
PARTE II
PARTE III

[EDIT: 17-05-2021]