Meccanica Statistica questa sconosciuta
Oggi vi voglio parlare della Meccanica Statistica, ovvero della sorellina minore, non per importanza scientifica sia ben chiaro, della più nota triade composta da Meccanica Classica, Meccanica Relativistica e Meccanica Quantistica.
La verità è che questo nome risulterà nuovo alla maggior parte di voi lettori appassionati di scienza, a meno che non abbiate seguito i corsi di fisica all’università ovviamente.
Il motivo è molto semplice: la Meccanica Statistica non è intuitiva come quella Classica, non ha portato a sensazionali rivolgimenti in grado di coinvolgere perfino la filosofia come quella Relativistica, non è circondata da quell’alone posticcio di pseudo mistero che avvolge quella Quantistica e forse a dirla tutta è pure un po’ timida.
Basti pensare a quale impatto mediatico abbiano avuto in questi anni le scoperte del Bosone di Higgs prima e delle Onde Gravitazionali poi mentre della Meccanica Statistica nessuna traccia.
Eppure uno dei più illustri scienziati contemporanei a livello internazionale, Giorgio Parisi, un fisico che per un soffio non ha ricevuto il Nobel ma che si è comunque guadagnato la Medaglia Boltzmann, ha dato enormi contributi al settore della fisica statistica.
Ed è questa una delle ragioni per cui voglio parlarvi di questo ambito di ricerca: l’altra ragione per cui voglio parlarvene è perché, nel mio piccolo, anche io me ne occupo. E fui sesto tra cotanto senno.
Ma partiamo dalle basi, ovvero dal nome. La Meccanica tradizionalmente studia il moto dei corpi, Newton docet. La Statistica, invece, è la scienza che studia con metodi matematici probabilistici i fenomeni collettivi.
Supponiamo ora di voler studiare un sistema composto da molti corpi , come per esempio un gas che è formato da un numero N di atomi dell’ordine di 1023, il numero di Avogadro: con un po’ di audacia potremmo definirlo un fenomeno collettivo della materia inorganica.
Se lo volessimo studiare secondo le leggi della fisica classica dovremmo considerare per ogni atomo la sua posizione e la sua velocità e risolvere 2N equazioni del moto per sapere come si muovono questi atomi nello spazio. Ma si presentano ben due problemi: innanzitutto è fisicamente impossibile misurare contemporaneamente velocità e posizione di così tanti atomi e in secondo luogo, fidatevi, neanche il più potente dei calcolatori odierni riuscirebbe in tempi umani a risolvere tutte quelle equazioni.
È chiaro: urge un cambiamento di approccio! Un piccolo aiuto può arrivare da una semplice considerazione. Riprendiamo il nostro gas all’equilibrio, cioè lasciato lì in pace, a farsi i fatti suoi dentro una bella ampolla grande, e misuriamo la temperatura e la pressione, che sono grandezze macroscopiche. Ora con un po’ di fantasia immaginiamo di poter spostare un solo atomo (o anche un paio) o di potergli cambiare la velocità: un atomo (o anche due) su 1023 non è per nulla determinante. Ciò che ci interessa, dunque, non è la posizione e la velocità esatta di ogni singolo atomo, ma la loro media su tutti i 1023 atomi.
Si parlerà quindi di distribuzione di probabilità delle velocità degli atomi, o distribuzione di Maxwell-Boltzmann: ed ecco che da un problema meccanico si è passati ad uno statistico.
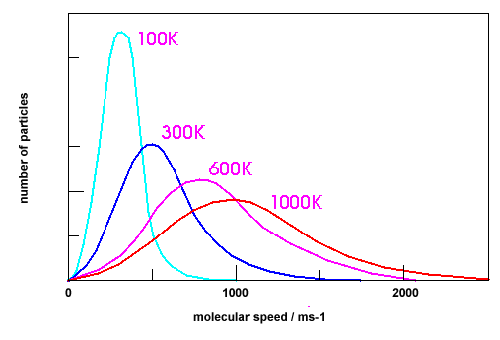
Un primo importantissimo risultato di questa teoria è che esiste un collegamento tra temperatura macroscopica del gas e velocità media microscopica degli atomi, ovvero quando la temperatura sale gli atomi si muovono più velocemente.
Ma proviamo a procedere un pochino più avanti.
Le posizioni e le velocità di tutti gli atomi nel sistema definiscono lo stato microscopico del nostro gas. Nello spazio ogni particella ha tre coordinate della posizione e tre coordinate della velocità: in totale ho 6N coordinate microscopiche del sistema.
Con una grande astrazione della mente, immaginiamo uno spazio a 6N dimensioni: ogni dimensione è una coordinata della posizione o della velocità di un atomo. Un punto in questo iperspazio, che viene chiamato spazio delle fasi, rappresenterà uno stato microscopico in cui può trovarsi il nostro sistema.
Ma abbiamo appena visto che cambiando un po’ la posizione o la velocità di alcuni atomi non cambia lo stato macroscopico del gas, definito, invece, dal valore dell’energia. Per un certo valore di energia ci saranno diversi stati microscopici corrispondenti. Questi stati sono rappresentati da diversi punti nello spazio delle fasi, disposti su un’ipersuperficie a energia costante immersa nell’iperspazio a 6N dimensioni, con una certa densità di probabilità che, nel caso di un gas in cui non si considerino gli effetti quantistici, è la distribuzione di Boltzmann. Il Postulato Fondamentale della Meccanica Statistica afferma che, quando il sistema è all’equilibrio, tutti gli stati microscopici corrispondenti ad un certo stato macroscopico di energia sono equiprobabili: cioè il sistema può trovarsi con la stessa probabilità in uno qualsiasi degli stati microscopici dell’insieme (ensemble).
Questo tipo di approccio, che si basa sulla valutazione di grandezze medie e sull’analisi statistica, può essere esteso a tutti i sistemi complessi, ovvero tutti i sistemi con un numero elevato di parti interagenti tra loro: quindi innanzitutto oltre i gas è possibile studiare con queste teorie i liquidi o i solidi, anch’essi costituiti da un grandissimo numero di molecole. Non solo: ritroviamo questo approccio nella modellizzazione dei cosiddetti fenomeni critici, ovvero le transizioni di fase della materia, tra cui importanza storica ha ricoperto la transizione ferromagnetica descritta dal celebre modello di Ising, o nel moto browniano, in cui le particelle di polline in acqua si muovono in modo disordinato e diffondono.
Ma le frontiere della ricerca si spingono molto più avanti.
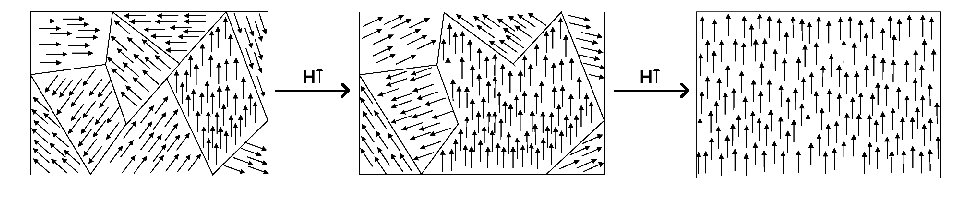
Vi ricordate all’inizio quando vi ho nominato il professor Giorgio Parisi? Ebbene Parisi è riuscito nel 1979 a trovare una soluzione all’equilibrio per un sistema di Spin Glass. Uno Spin Glass, o vetro di spin, è un magnete disordinato caratterizzato da interazioni frustrate, cioè nelle quali i vettori momento magnetico degli atomi non sono allineati in un reticolo preciso e ci sono sia legami tra atomi con stesso momento magnetico che con momento magnetico opposto.
Le teorie della meccanica statistica sono state utilizzate per modellizzare il comportamento di materiali superconduttori che, tra le altre applicazioni, sono impiegati negli acceleratori di particelle: tra tutti ricordiamo i magneti superconduttori degli esperimenti LHC e CMS del CERN di Ginevra che hanno portato alla scoperta del Bosone di Higgs.


Presso l’Università La Sapienza di Roma, il gruppo del professor Cavagna e della professoressa Giardina (COBBS LAB) sta portando avanti una linea di ricerca di recente sviluppo ma che si è già guadagnata diverse copertine sulla rivista Nature per la sua originalità e innovazione, oltre che per gli ottimi risultati ottenuti. Si tratta dello studio del comportamento collettivo di stormi di uccelli e di sciami di insetti e dello sviluppo di un modello che spieghi il meccanismo delle loro evoluzioni spettacolari.
Lo sviluppo della ricerca in Meccanica Statistica è legato anche allo studio delle reti complesse e tra queste oggi stanno avendo un grande successo le reti neurali per il loro collegamento con il machine learning e l’intelligenza artificiale. Infatti la rete di Hopfield, la rete neurale artificiale in grado di simulare la capacità umana di ricordare le cose e di riconoscere immagini distorte, non è altro che un’applicazione del modello di Ising, modello nato per descrivere la transizione ferromagnetica. Ma ci sono anche importantissime applicazioni nell’ambito delle neuroscienze. In particolare con modelli statistici è stato studiato il comportamento collettivo e auto-organizzativo di una rete di neuroni, l’attività elettrica di un singolo neurone e la capacità dei neuroni di ricordare.
Crediti: FOTO IN COPERTINA

