Le figure impossibili: un pensiero di Penrose e l’arte di Escher
Salve a tutti, nello #SciPho di oggi parliamo di “figure impossibili” e iniziamo proprio introducendo uno degli artisti più emblematici: Maurits Cornelis Escher (1898- 1972) il quale, a cavallo tra Arte e Matematica, viene spesso ricordato per la particolare riflessione geometrica, simmetrica, paradossale e metamorfica nelle proprie opere.
Sebbene durante l’arco della sua vita Escher abbia sempre ammesso un’ignoranza per le teorie matematiche a lui contemporanee, in realtà le sue opere si sono presto trovate in un rapporto di simbiosi con il mondo della matematica, della fisica e della filosofia: moltissimi scienziati, contemporanei all’artista e non, trovano nella sua arte una rappresentazione pittoresca di concetti astratti e affascinanti e non di rado anche ispirazioni per il proprio lavoro.
Un esempio della bellezza e dell’importanza del lavoro di Escher ci viene da Sir Roger Penrose (1931): importantissimo matematico, fisico e cosmologo contemporaneo. Il famoso “triangolo di Penrose” è un esempio di ciò che viene chiamato oggetto impossibile, ovvero un oggetto che può essere rappresentato solo in maniera bidimensionale e che quindi non può trovare una sua costruzione nello spazio.
Questa figura impossibile è stata di ispirazione per Escher:

Nel 1992 Penrose ha pubblicato un articolo “On the cohomology of impossible figures” ovvero “Sulla coomologia delle figure impossibili”. All’interno di questo articolo Penrose è riuscito a descrivere, con una grandissima intuizione figurativa, un concetto fondamentale all’interno di molte teorie matematiche contemporanee: la coomologia dei fasci.
Su cosa sia questa coomologia cerchiamo di dare subito una risposta: prendiamo un certo dato associato ad un oggetto geometrico X (da pensare come “uno spazio”), in che modo si può, se si può, avere qualche informazione sul dato o sul nostro oggetto geometrico a partire dalle informazioni sull’altro? Possiamo associare al nostro spazio degli invarianti algebrici, ovvero degli oggetti di natura algebrica (in cui si può moltiplicare, addizionare etc…) che quantificano parte dell’informazione contenuta nello spazio e dopodiché cercare di studiare le proprietà che questo invariante possiede: esso infatti potrebbe dirci molto sia sullo spazio sia sui dati che vogliamo studiare. La ricerca “dell’invariante perfetto” che possa distinguere qualsiasi tipo di dato su ogni tipo di oggetto geometrico è qualcosa di troppo ambizioso, data la generalità della geometria. Si utilizzano quindi invarianti in base al tipo di problema che si sta affrontando: alcuni di questi sono chiamati “teorie di coomologia”. Un punto importante è che i tipi di dati che possiamo studiare su un oggetto geometrico sono di ogni natura: possono essere equazioni, possono essere altri oggetti geometrici sopra di esso.
Che cosa intende dire Penrose con “la coomologia delle figure impossibili”?
Penrose, all’interno del suo articolo, descrive un processo di costruzione di una “teoria di coomologia” delle figure impossibili basata sulla “prospettiva”. Infatti, sebbene il triangolo di Penrose sia a tutti gli effetti un oggetto impossibile, è comunque possibile realizzarlo in tre dimensioni grazie a dei giochi di prospettiva: distorcendo la distanze tra i tre lati del triangolo, si può quindi creare una situazione per la quale un dato osservatore può vedere il triangolo di Penrose.

Questa idea si può descrivere in maniera un po’ più generale: presa una figura impossibile disegnata, si può cercare di suddividerla in varie “aree”, le quali sono tutte singolarmente realizzabili nello spazio (per il triangolo di Penrose queste aree erano i tre lati presi singolarmente) e dopodiché utilizzare la prospettiva per creare l’effetto ottico della figura impossibile. Ciò che vuole sottolineare Penrose è che una figura impossibile può (talvolta, esclusi casi più estremi) essere immaginata come una figura che localmente è perfettamente possibile, ma che può essere realizzata solamente tramite incollamenti che nello spazio non possono essere effettuati. La “coomologia” che viene descritta da Penrose è infatti basata sul calcolo delle distanze delle aree scelte e messe in prospettiva con l’osservatore, il rapporto di queste distanze può essere sostanzialmente di due tipi: o le distanze possono essere contemporaneamente riscalate tutte e risultare quindi uguali, oppure le distanze sono in un certo qual modo “eterogenee” e non permettono di essere riscalate in un modo uniforme ottenendo un’uguaglianza. Nel primo caso si ha che l’oggetto che si voleva descrivere è un oggetto possibile, mentre nel secondo caso si hanno le figure impossibili. La classe a cui appartiene l’oggetto è detta quindi la “classe di coomologia”.
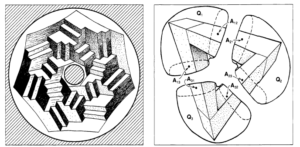
Questo metodo di studiare classi di nuovi oggetti geometrici globali costruiti a partire da relazioni locali definite su porzioni dello spazio di partenza è un modo intuitivo di descrivere l’approccio della coomologia dei fasci la quale cerca di classificare oggetti di tipo geometrico (e non) a partire da comportamenti locali e incollamenti.



