Cos’è il campo gravitazionale?
Che si parli di Relatività Generale o di meccanica classica, si sente sempre nominare questo misterioso “campo gravitazionale”. Ma che cosa indica questo concetto?
Una massa qualunque, come ad esempio la Terra o un altro corpo celeste, attrae a sé tutto ciò che la circonda attraverso la forza di gravità. Questa forza è descritta, nel caso più semplice, dalla Legge di Gravitazione Universale. Il campo gravitazionale è una funzione matematica che descrive come una massa alteri lo spazio circostante; ossia, data una massa ed il suo campo gravitazionale, siamo in grado di calcolare la forza di gravità che questa genera in ogni punto dello spazio.
Vogliamo studiare il campo gravitazionale generato da una massa che chiamiamo M, ad esempio la massa terrestre. Prendiamo poi una massa di prova m, una massa così piccola da non modificare in misura consistente il campo generato dalla Terra, per esempio una biglia. Spostando la biglia idealmente in tutti i punti dello spazio possiamo misurare la forza di gravità generata dalla Terra in tutti questi punti.
Dalla Legge di Gravitazione Universale

sappiamo che la forza di gravità (newtoniana) è proporzionale al prodotto della massa terrestre M e della massa di prova m diviso il quadrato della loro distanza. Dividendo questo valore per il valore di m otteniamo quindi una quantità indipendente dalla massa di prova, e questa quantità la chiamiamo campo gravitazionale.
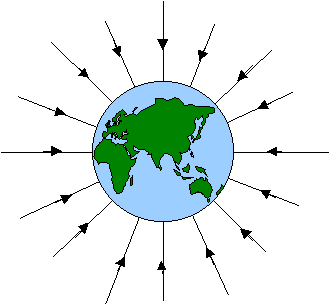
La forza di gravità è sempre attrattiva, ed è quindi diretta verso il centro della Terra. Possiamo tracciare una serie di linee, dette linee di campo, che indicano la direzione ed il verso che l’attrazione segue.
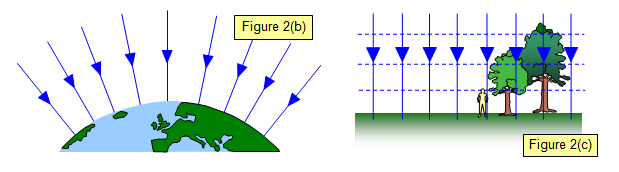
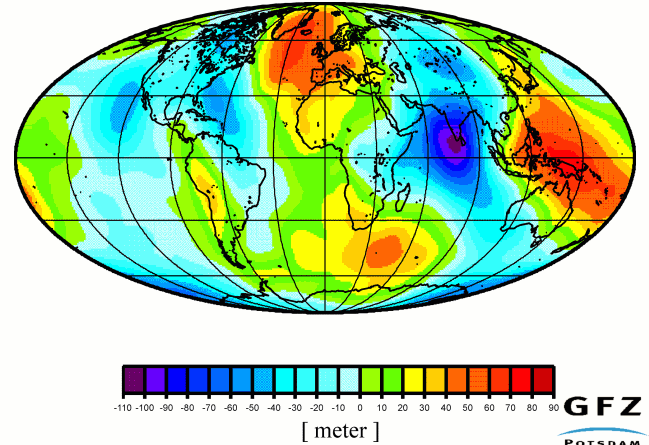
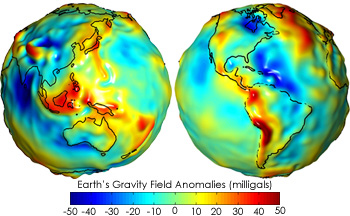
Il campo gravitazionale così disegnato e calcolato è una versione estremamente semplificata della realtà: abbiamo infatti assunto che la massa sia completamente concentrata in un punto, il centro della Terra, e questa assunzione è valida solo se la distribuzione di massa è perfettamente sferica, ossia se la Terra fosse una sfera e la sua massa fosse completamente omogenea. Ma la Terra, così come gli altri corpi celesti, è in realtà schiacciata ai poli e rigonfia all’equatore, ha depressioni e montagne e una composizione interna tutt’altro che omogenea. L’approssimazione vale allora solo se ci allontaniamo a sufficienza dalla Terra così da “non vedere” le irregolarità, cosa che rende efficacie lo studio del moto dei pianeti tramite la Legge di Gravitazione Universale.
Quando andiamo più vicino, però, come nel caso di un satellite in bassa orbita terrestre, la faccenda si fa più complicata, ed occorre considerare le irregolarità per avere un calcolo più preciso del campo gravitazionale. Questo si fa andando ad aggiungere alle equazioni della gravità ricavate dalla Legge di Gravitazione Universale altri elementi, noti come armoniche sferiche, che creano un approssimazione via via migliore del campo. La conoscenza di queste armoniche sferiche è fondamentale per il corretto calcolo delle orbite che devono seguire i satelliti.
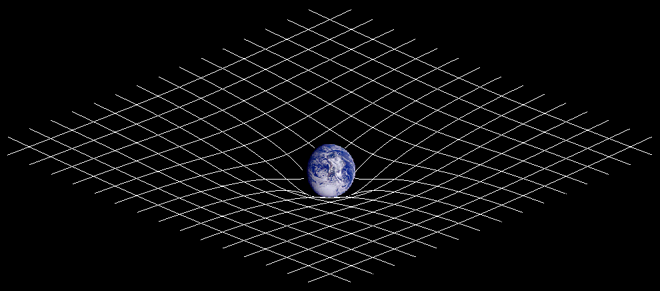
Il campo gravitazionale di cui abbiamo parlato finora, quello della meccanica classica newtoniana, non ha però una causa ben definita. Una massa attrae le altre, ma il perché non era ben chiaro. Entrando nell’ambito della Relatività Generale, tale causa diventa un po’ più chiara: una massa posta nel tessuto dello spazio-tempo lo deforma e le altre masse si muovono all’interno di tale deformazione. In questo caso, la massa di prova è una massa che non è in grado di deformare lo spazio-tempo tanto da interferire con la deformazione della massa terrestre. L’approssimazione newtoniana continua comunque ad essere valida finché non ci troviamo in presenza di masse molto grandi, come nei pressi di una stella o di un buco nero.