“Cosa è un punto?”, Geometria NonCommutativa I: Teoria delle Categorie

“Cosa è un punto?” Geometria Noncommutativa è una serie di articoli che cercano di introdurre, in maniera divulgativa, un ambito della Matematica, esteso per quanto concerne il punto di vista interpretativo, motivato dalla necessità di chiarire la missione senza fine che è la comprensione dei principi primi della geometria.

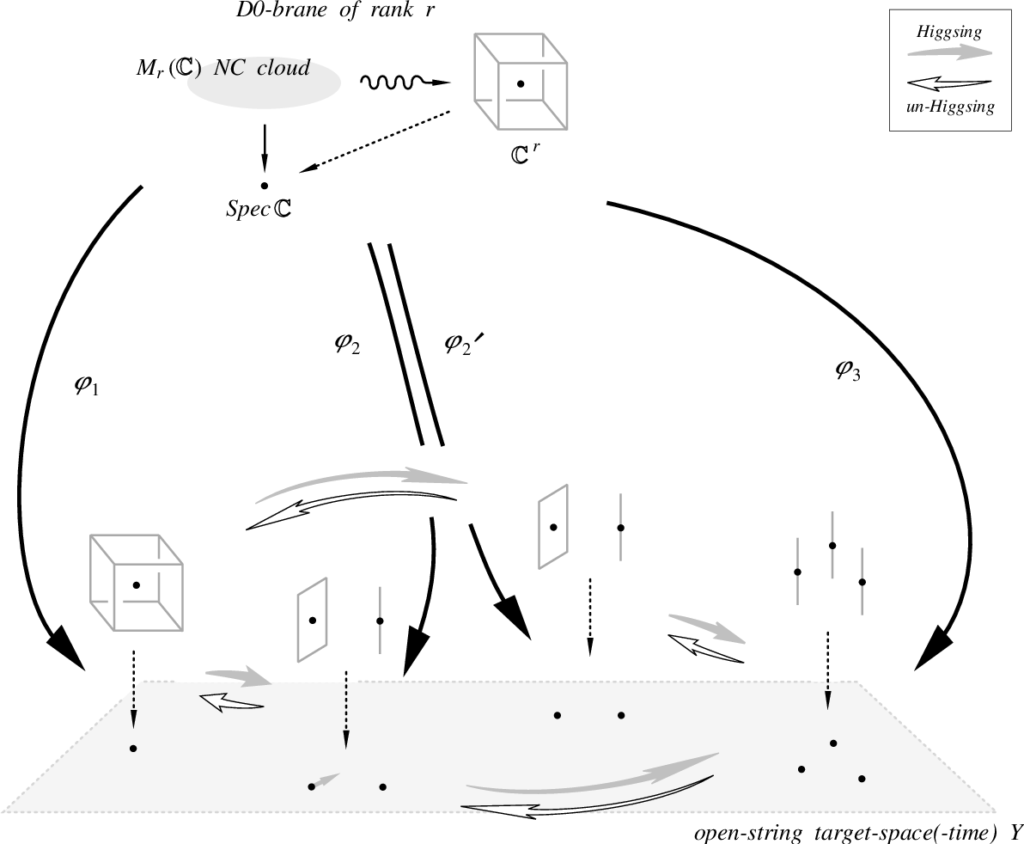
Nell’articolo “Perché investire soldi nell’astratto? L’utilità della teoria“, scritto insieme a Davide Bufalini, viene spiegato come mai gli strumenti astratti che abbiamo sviluppato (in Matematica e Fisica Teorica, ma non solo) siano di centrale importanza nello sviluppo della nostra civiltà ed è in questo spirito che questa rubrica si propone: è importante capire quali siano i perché dietro una teoria che sta coinvolgendo sempre più discipline.

In questa prima introduzione vedremo rapidamente il concetto di Categoria, che riprenderemo spesso nei prossimi articoli e che approfondiremo quando necessario. Se quindi questa introduzione vi sembra ancora poco contestualizzata, in realtà riguarda una delle colonne portanti della riflessione Matematica attuale.

Perché?

Già dagli albori della Matematica il concetto di punto in geometria è stato oggetto di discussione. Infatti, il suo carattere di “ente primitivo” è indice dell’idea di geometria sulla quale costruiamo le idee.

Euclide, negli Elementi, indica il punto come “ciò che non ha parti”. Questo modo di indicare il punto è sicuramente efficace dal punto di vista intuitivo, ma dal punto di vista formale, in mancanza di qualsiasi contesto, è un’indicazione inutile. Contestualizzando, seguendo il ragionamento di Cartier, per Euclide ciò che esiste sono le figure geometriche e un punto è caratterizzato dall’essere l’ente elementare di queste figure. In questo contesto c’è una relazione genetica tra le varie figure: una figura può generarne un’altra. Si pensi ad esempio alle definizione di retta come figura generata da due punti.

Dal punto di vista moderno, i punti sono assunti esistenti e sono soggetti a relazioni, un punto di vista che indicheremo come ontologico.

La geometria si è sviluppata in maniera considerevole e ad oggi è una delle branche più estese della Matematica, con collegamenti molto stretti con la Fisica (e.g. Meccanica Quantistica, Relatività, Meccanica Razionale, Meccanica Statistica, Astrofisica, etc…), per questo motivo il punto di vista dal quale guardare gli oggetti geometrici è estremamente importante per dare letture nuove a problemi di ambito matematico e fisico.

Teoria delle Categorie.

L’interesse per la teoria delle categorie è nato dalla considerazione che molte strutture utilizzate in Matematica, in qualsiasi campo, non sono poi così diverse. Infatti, diversi oggetti utilizzati in teorie diverse, o nella stessa teoria, si “comportano” in maniera simile. Questa considerazione è accompagnata da una naturale necessità di contestualizzare, in un ambiente ben specificato, questi oggetti simili e studiarne le proprietà. In questo modo intere teorie possono essere comprese meglio, semplificate e ripulite, perché si riesce ad andare a fondo nella struttura primaria delle cose.

La teoria delle categorie è stata introdotta da Samuel Eilenberg e Saunders Mac Lane nel 1942/45 per studiare alcuni aspetti della topologia algebrica: questo è l’ambito nel quale la teoria delle categorie ha dapprima trovato applicazioni serie e tutt’ora è uno strumento potentissimo utilizzato da chi lavora in questo ambito.

Oltre agli ambiti in Matematica e in Fisica in cui la teoria delle categorie si è rivelata estremamente utile, il cambio di prospettiva offerto dall’ambito è stato di ispirazione anche in campi come la biologia (2), linguistica, informatica teorica e nello studio degli algoritmi.

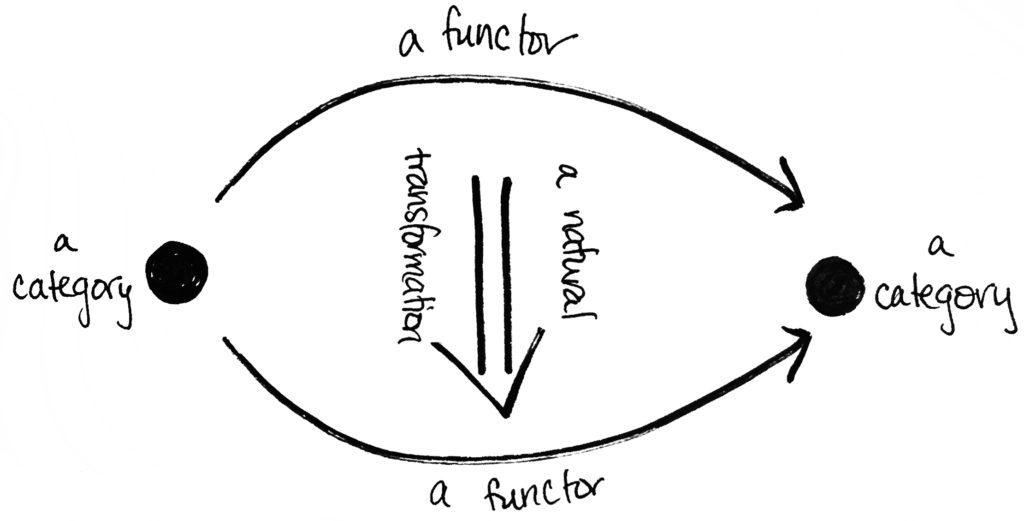
I concetti fondamentali della teoria sono tre: Categorie, Funtori, Trasformazioni Naturali.

Consideriamo il seguente esempio, che porta alla mente ricordi delle scuole elementari:

Immaginiamo di avere un cesto di 10 caramelle e di doverle distribuire a 5 bambini in maniera omogenea, quante caramelle andranno a ciascuno di essi?

Questo problema è realmente elementare, ma si presta subito ad essere generalizzato. Se infatti abbiamo il cesto con 10 caramelle dentro e dobbiamo distribuirle a 5 bambini in maniera totalmente libera, ovviamente non ci sarà una quantità specificata di caramelle per ogni bambino, ma questa può variare in base all’assegnazione che facciamo (chiamata funzione) e conseguentemente avremo una certa quantità di funzioni associate a questo problema (5 elevato alla 10, se consideriamo le caramelle tutte diverse tra loro).

Il problema di capire quali siano le funzioni tra l’insieme delle caramelle e l’insieme dei bambini è indipendente dal fatto che il primo insieme sia di caramelle e il secondo di bambini, ma dipende unicamente dalla quantità di elementi che ogni insieme ha. Nel caso precedente erano 10 uno e 5 l’altro, ma in generale possiamo dire che il primo insieme possa avere n elementi e il secondo m.

Cosa ci abbiamo guadagnato? Abbiamo capito che il nostro problema, molto particolareggiato in dettagli, è in realtà di natura molto più generale e quindi, tramite lo stesso procedimento utilizzato per risolverlo, possiamo risolvere una classe di problemi ben più ampia.

Quale classe?

La classe che consideriamo è quella degli insiemi finiti. Ovvero consideriamo l’insieme (infinito) degli insiemi finiti. Questo insieme ha come elementi gli insiemi finiti. Dal momento che abbiamo scoperto che il nostro problema è indipendente dal tipo di insieme, ma dipende solo dal numero degli elementi che contiene, allora invece di prendere tutti gli insiemi finiti, possiamo prenderne uno per ogni numero finito (che sarà il numero di elementi che contiene).

Indicheremo un insieme finito in base al numero di elementi che ha, quindi se ha 10 elementi lo chiameremo “10“, più in generale se ha m elementi lo indicheremo “m“. Ora dati n ed m, possiamo chiederci quali sono le funzioni tra n ed m, questo è un insieme e lo indichiamo con Map(n,m) (da mappa, i.e. funzione).

Cosa possiamo dire su questi insiemi Map(n,m) ? Sicuramente che se consideriamo n=m, ovvero Map(n,n), allora questo contiene una funzione in un qualche modo speciale, chiamata funzione identità, questa funzione lascia tutto invariato, ovvero prende l’insieme di n elementi e manda ogni elemento in se stesso, senza cambiarlo.

Inoltre se prendiamo una funzione in Map(n,m) e una in Map(m,r) allora possiamo applicare prima la prima funzione e poi la seconda ed ottenere una funzione che va da n ad r, ovvero in Map(n,r). Questo processo è chiamato composizione.

La funzione identica ha la, ovvia, proprietà che quando composta con altre funzioni, allora non le cambia.

Quindi ricapitolando, abbiamo: Una classe di oggetti – Insiemi finiti (1,2,3,…) –

Una classe di funzioni – Map(n,m) – per ogni coppia di insiemi finiti.

Queste due strutture sono tali che ci sono le funzioni identità e le funzioni possono essere composte (associativamente) quando il codominio della prima coincide con il dominio della seconda.

Questa struttura è un esempio di Categoria, che nel libro di Eilenberg – MacLane (Categories for the Working Mathematician), è indicata con FinOrd (da finite ordinals).

Più in generale, se specifichiamo una classe di oggetti e una classe di funzioni, che in teoria delle categorie sono chiamate morfismi, in maniera tale che esistano le funzioni identità e che coppie di funzioni in cui il codominio della prima coincide con il dominio della seconda possano essere composte (associativamente), allora siamo in presenza di una Categoria.

Quali sono esempi di categorie?

Un esempio lo abbiamo visto, ma cosa ci ferma dal considerare la categoria di tutti gli insiemi? Nessuno e infatti questa è una categoria. Si noti comunque che la classe di tutti gli insiemi non è un insieme (questo è il famoso paradosso di Russell), ma comunque sia in teoria delle categorie non è necessario considerare insiemi di oggetti e insiemi di morfismi, per questo invece di usare la parola insieme, si usa la parola classe. La categoria di tutti gli insiemi è indicata con Sets.

Ci sono altre categorie che chi abbia conoscenze di Geometria o Algebra, può riconoscere:

• La categoria vuota: nessun oggetto, nessun morfismo.
• La categoria con un solo oggetto ed un solo morfismo (identità).
• La categoria degli spazi vettoriali di dimensione finita un campo fissato. La classe dei morfismi sono le mappe lineare, aka matrici.
• La categoria dei gruppi con morfismi gli omomorfismi tra gruppi.
• La categoria degli spazi topologici con morfismi le funzioni continue tra questi.

Come confrontare due categorie?

Questa domanda si traduce nella domanda: possiamo definire funzioni tra due categorie?

La risposta è sì, ed è il concetto di funtore.

Un funtore è proprio una funzione tra categorie: assegna ad ogni oggetto di una categoria di partenza, un oggetto di quella di arrivo e ad ogni morfismo tra due oggetti nella categoria di partenza un morfismo nella categoria di arrivo. Ovviamente un funtore deve soddisfare delle proprietà ulteriori, altrimenti sarebbe un oggetto che non tiene conto di tutta la struttura che una categoria ha. Infatti un funtore deve mandare i morfismi identità in morfismi identità e deve essere tale che la composizione di morfismi venga preservata dal funtore (ovvero se f,g sono morfismi nella categoria di partenza e h è la funzione composta di f e g, detto F il funtore, si ha che F(f) composto F(g) deve essere F(h)).

I funtori si distinguono in covarianti (mantengono il verso dei morfismi) o controvarianti (invertono il senso dei morfismi).

Il concetto di trasformazione naturale è un concetto ulteriore, che può essere pensato come “funzione tra due funtori” , ma dal momento che ora non ci serve, non daremo la definizione. Ciò che daremo invece è un esempio (un po’ tecnico) di struttura Categorie, Funtori, Trasformazione Naturale.

Si considerino due categorie: la categoria degli anelli commutativi e la categoria dei gruppi, ci sono due funtori tra queste due categorie. Il primo manda ogni anello commutativo nel gruppo delle matrici, su quell'anello, di ordine n invertibili (GL(n,K)), l'altro funtore associa ad ogni anello commutativo il gruppo delle unità di quell'anello (K*). Allora il determinante è una trasformazione naturale tra questi due funtori.