Dove sono finiti i LEM delle missioni Apollo?

I resti dei LEM non andrebbero cercati intorno alla Luna, ma sul suo suolo.
La causa non è da cercarsi in un’atmosfera di cui si ignorava l’esistenza, ma nel campo gravitazionale della Luna che è tutt’altro che sferico. Armati di un po’ di matematica, vediamo come si potrebbe fare in modo che i satelliti restino in orbita senza ricadere sulla Luna.

Ciò non dovrebbe far stupire dato che anche con telescopi amatoriali si può apprezzare quanto siano evidenti i rilievi montuosi rispetto all’orizzonte della Luna.

È possibile prevedere come varierà il campo gravitazionale della Luna per mantenere in orbita un satellite? Sì, e per questo bisogna dare una descrizione molto più accurata rispetto a quella di un semplice campo sferico. Vediamo insieme come!

Un Modello per la forma della Luna

È necessario comprendere le cause dell’attuale forma della Luna per poterla descrivere coscientemente. Come per qualsiasi corpo celeste, è il risultato dell’azione di più forze. La più importante è sicuramente l’azione della Forza di Gravità che mantiene aggregato il corpo. Successivamente fra le forze più deboli spicca la Forza Centrifuga, che schiaccia i corpi celesti ai poli tanto più ruotano velocemente. Nel caso di corpi celesti vicini fra loro come pianeti e satelliti c’è anche da considerare l’azione delle Forze Mareali. Sono sempre forze di natura gravitazionale e tendono a stirare la forma verso la direzione congiungente i due corpi. Infatti così come la Luna esercita sulla Terra delle forze mareali in grado di sposare le masse liquide, così la Terra esercita sulla Luna delle forze mareali in grado di deformarne le rocce.

Sono la causa della risonanza orbitale del moto lunare. Infine le imperfezioni superficiali dovute agli innumerevoli impatti meteorici che a causa dell’inesistente attività tettonica non sono stati distrutti nel tempo.

L’Ellissoide di Riferimento

Possiamo osservare come la forma evolva da quella sferica andando a sommare consecutivamente queste 3 forze. Per comprendere meglio immaginiamo di prendere come riferimento 3 raggi della sfera perpendicolari fra loro. Uno in direzione del polo nord C, e due nelle direzioni perpendicolari fra loro sull’equatore che chiamiamo A e B. Questi raggi descrivono i semiassi principali di un ellissoide, per ora degenerati in una sfera (dunque sono tutti e 3 uguali). Sommando la forza centrifuga a quella gravitazionale si ha un primo schiacciamento della sfera in direzione dell’asse polare. Dunque troveremo che C è più corto di A e B (che sono aumentati per mantenere il volume costante). Questa forma è anche chiamata Sferoide Oblato. Aggiungendo l’azione delle forze mareali avremo che anche A e B saranno diversi. Se questa forza fosse in direzione di A, avremo che A cresce mentre B e C diminuiscono, e C sarebbe il minore di tutti.

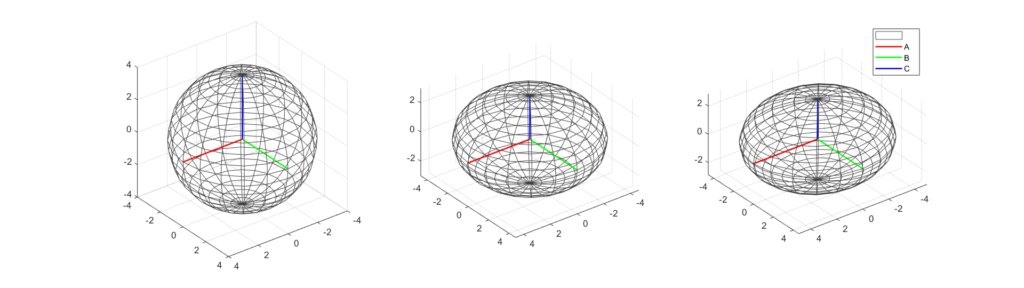
Il Tensore di Inerzia

Matematicamente parlando, queste azioni vanno a deformare la distribuzione della massa nello spazio, che verrà descritta attraverso il Tensore di Inerzia. Si tratta di un oggetto matematico che racchiude le informazioni su come la massa di un corpo è distribuita nello spazio. È descritto da una matrice di tre righe e tre colonne (dato che ci troviamo in uno spazio tridimensionale), che racchiude 9 numeri, chiamati componenti. Andranno a descrivere la distribuzione di massa nello spazio ognuna rispetto una direzione.

Se ci poniamo nel sistema di riferimento descritto dai raggi A B C, delle 9 componenti ne sopravvivono solo 3, che verranno chiamate le componenti principali del tensore. Queste componenti principali di inerzia non sono altro che i 3 momenti di Inerzia I₁, I₂, I₃ rispettivamente verso A B C. Fermandoci qui, otterremmo una descrizione del campo gravitazionale che ci fornisce l’Ellissoide di Riferimento.

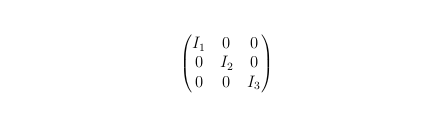
Forme Irregolari descritte da Oggetti Armonici

Alla descrizione del campo gravitazionale fornita dall’ellissoide d’inerzia si possono aggiungere anche i contributi dovuti ai rilievi e alle depressioni date dagli innumerevoli crateri, grazie allo strumento matematico dello Sviluppo in Armoniche Sferiche. Sommando particolari polinomi omogenei detti Polinomi di Legendre Associati di grado “L”. Il loro contributo totale al campo avrà un peso tanto minore quanto il grado “L” è elevato. Si tratta di uno strumento molto potente, usato anche in altri settori come nella meccanica quantistica per descrivere gli orbitali atomici. Ad esempio n, il numero quantico principale prende il posto di L. Proprio come avviene per i numeri quantici dell’atomo, a ogni grado L si possono inserire 2L+1 polinomi, ognuno di indice m, detto indice magnetico. Quindi il numero di polinomi da poter aggiungere a ogni grado è proporzionale al grado stesso. Rimanendo nel campo dell’astrofisica, è usato anche nel descrivere i campi magnetici planetari.

Questi polinomi ospitano al loro interno dei coefficienti estrapolati da dati procurati da misure dirette. Ad esempio una mappa molto accurata è stata descritta dalla missione GRAIL [Gravity Recovery And Interior Laboratory]: una costellazione di 2 satelliti che orbitando intorno alla Luna vicini fra loro hanno potuto misurare la variazione del campo gravitazionale locale della Luna. La mappa GRGM1200A. ospita coefficienti per polinomi fino al grado 1200, permettendo di rendere evidenti dettagli con una scala spaziale di circa 4,45 km. Fra i coefficienti di grado 2 del campo gravitazionale, spicca fra tutti quello chiamato J₂ che è in stretta relazione con i momenti di inerzia principali.

Il contributo di queste descrizioni sempre più accurate ha potuto determinare una forma sempre più accurata per il campo gravitazionale lunare e alla forma della Luna: l’equivalente lunare per il geoide terrestre [selenoide?], che altri non è che una superficie equipotenziale del campo gravitazionale.

Come si comporterebbe un satellite che descrive un’orbita circolare bassa intorno la Luna?

L’accelerazione centrifuga dovuta al moto orbitale non sarebbe più controbilanciata punto per punto dall’accelerazione gravitazionale, generando delle forze inerziali che tendono a modificare l’orbita. Dopo molti giri, l’orbita risulterà fortemente cambiata e l’energia del sistema non farà altro che diminuire, causando la deorbitazione del satellite.

Questo è il motivo per cui i satelliti artificiali possono avere in dotazione dei propulsori elettrici dalla spinta molto piccola ma in grado di operare a lungo per correggere costantemente l’orbita e mantenerla stabile. Vi avevamo parlato in dettaglio della tipologia usata per questo scopo gli [HET] nel nostro approfondimento sulla propulsione al plasma.

In realtà di LEM ne rimane uno! Snoopy della missione Apollo 10 che vedete nell’immagine di copertina. Sganciato dopo i test in orbita lunare con il propulsore acceso, è uscito dal campo gravitazionale della Terra per entrare in orbita attorno al Sole!

Oltre a lui non hanno subito lo stesso destino il modulo Eagle dell’Apollo 11, che è stato fatto schiantare volutamente sulla superficie lunare per ottenere dati dai sismografi, e quello dell’Apollo 13, che è bruciato nell’atmosfera terrestre dopo aver fatto da scialuppa di salvataggio.