Sotto terra la gravità è più forte?

Luca Nardi Novembre 7, 2020Novembre 7, 2020 0 Commenti accelerazione gravitazionale, gravità, Terra

A volte l’intuizione fa cilecca. Potremmo pensare che siccome la gravità attira i corpi verso il centro della Terra, più andiamo in profondità maggiore sarà l’attrazione gravitazionale. Eppure le cose non vanno esattamente così.

Quando deve affrontare un problema di qualsiasi natura, un fisico ragiona per livelli successivi di complessità. Si parte dal problema nel caso più semplice possibile, e poi lo si complica fino al punto che occorre per descrivere bene un particolare aspetto della realtà. Per esempio, se si vuole studiare il moto di un mucchio di sabbia, si potrebbe partire da granelli sferici e tutti di un’unica dimensione, per poi andare a complicarne mano mano la forma e le possibili dimensioni che possono avere.

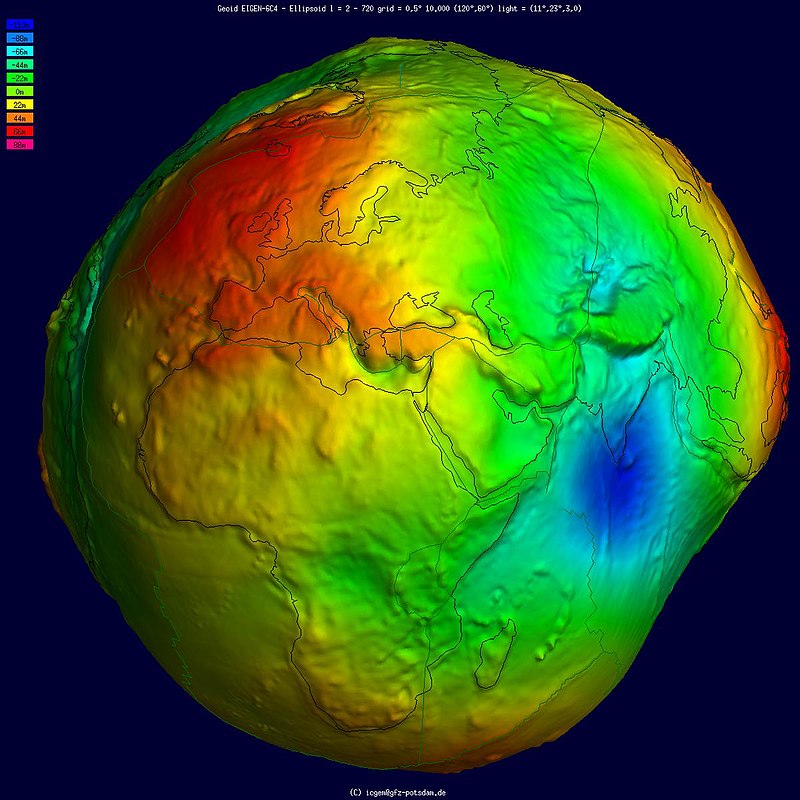
In maniera simile, per affrontare il problema della gravità “sotterranea”, partiamo da una Terra completamente sferica. La Terra è sferica solo in prima approssimazione, la si descrive meglio come uno sferoide oblato (una sfera schiacciata ai poli e tirata all’equatore), ancor meglio come un geoide (che descrive la superficie media degli oceani se non si considerano maree e venti), e la perfezione si raggiunge considerando anche tutte le irregolarità della superficie, come i rilievi e le fosse. Ma noi partiamo da una Terra sferica, perché è quella che ci occorre per affrontare il problema iniziale nella maniera più semplice: sotto Terra la gravità è più o meno forte di quella che un corpo subisce sulla superficie?

Il geoide terrestre, esagerando i dislivelli tra i vari punti. Credits: ICGEM

La forza di gravità

Una massa qualunque, come ad esempio la Terra o un altro corpo celeste, attrae a sé tutto ciò che la circonda attraverso la forza di gravità. Questa forza chiama in ballo la Relatività Generale ma nel caso più semplice in cui ci siamo posti, ossia quello di una Terra completamente sferica (e omogenea, ossia senza variazioni di densità e composizione), è ben descritta dalla Legge di Gravitazione Universale di Newton. Se la Terra è sferica, e se inseriamo un corpo altrettanto sferico – per esempio una biglia – nella sua sfera di influenza gravitazionale, tale corpo subisce la forza come se la massa della Terra fosse concentrata in un solo punto, nel suo centro.

La legge di gravitazione universale descrive la forza gravitazionale esercitata tra la Terra (sferica) e la biglia. La forza dipende unicamente dalle masse dei due corpi e dalla loro distanza reciproca.

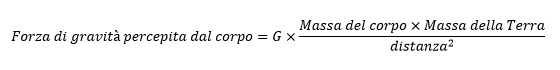
Siccome le masse e la costante G (la costante di gravitazione universale) sono fissate, il valore della distanza dal centro della Terra è l’unica cosa che può variare: si dice allora che la forza di attrazione gravitazionale si riduce come il quadrato della distanza, ossia più la massa della biglia è lontana dal centro della Terra, molto meno intensa sarà la forza con cui la Terra la attrae. Se mettiamo la biglia esattamente sulla superficie terrestre, la distanza è il raggio della Terra e si ottiene la forza di gravità che percepiamo anche noi esseri che vi camminiamo sopra.

La legge di gravitazione universale, nel caso di terra perfettamente sferica, è valida sicuramente dalla superficie terrestre fino a una distanza infinita. Ma se proviamo a spostarci all’interno della Terra, supponendo che la biglia si possa mettere in una posizione qualunque del nostro pianeta mantenendosi integra, come possiamo ragionare per calcolare la forza di gravità?

E dentro la Terra?

In generale, se ci sono più masse a generare gravità, l’attrazione subita da un corpo è data dalla somma delle forze di gravità generate da tutte masse che lo circondano.

Per semplificarci la vita, quando la biglia si trova dentro la Terra possiamo quindi immaginare di dividere la massa della Terra in due parti: la massa che si trova a profondità maggiori di quelle a cui si trova la biglia, e la massa che si trova all’esterno rispetto alla posizione della biglia, un guscio sferico che circonda la prima sfera.

Per fare un esempio molto pratico: la Terra ha un raggio di 6400 chilometri, possiamo mettere la biglia a 5000 chilometri dal centro della Terra. La sfera interna sarà tutta la massa compresa tra il centro e 5000 chilometri, la massa esterna tutta quella tra 5000 chilometri e 6400 chilometri. Sommando la forza di gravità generata da queste due porzioni di Terra sul corpo, otteniamo la forza totale che il corpo subisce.

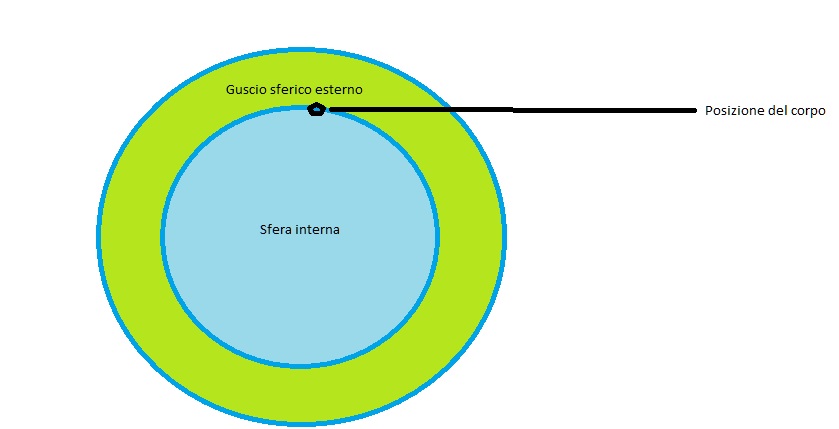
Per la sfera interna il ragionamento è lo stesso del corpo esterno alla Terra sferica: la sfera interna è come se fosse una Terra più piccola e quindi si può applicare senza problemi la legge di gravitazione universale. Siccome in questo caso la sfera ha una massa minore del raggio terrestre, l’attrazione gravitazionale che genera sul corpo è minore.

Per quanto riguarda il guscio esterno, invece, la cosa è un po’ più complicata. Non possiamo applicare la legge di gravitazione universale per l’intera massa del guscio esterno, perché il guscio non è un corpo sferico ma è, appunto, un guscio.

Tiro alla fune gravitazionale

Per il guscio sferico ragioniamo diversamente: pensiamo che la forza di gravità che la biglia subisce è data dalla somma della forza di gravità che ogni particella del guscio esercita sulla biglia. Ognuna di queste particelle si trova a una distanza diversa dalla biglia, e pertanto esercita una forza di gravità differente su di essa: le particelle più vicine eserciteranno una forza più intensa, quelle più lontane una forza meno intensa.

Questo problema è risolto dal cosiddetto “teorema dei gusci”, postulato dallo stesso Newton: un guscio sferico non esercita alcuna forza gravitazionale sui corpi che vi si trovano all’interno. Ogni sezione del guscio attira infatti verso sé la nostra biglia, ma per ogni sezione ve ne è un’altra dal lato opposto che attira in misura uguale e contraria la biglia dall’altra parte.

La *potente* simulazione grafica qui sopra ci può venire in aiuto: rappresenta una sezione della Terra in cui la biglia si trova nel punto indicato dalla riga nera. Il guscio sferico è verde, la sfera interna è azzurra. La regione viola e quella rossa sono messe in evidenza per una ragione ben specifica: le particelle che si trovano nella regione viola attraggono la biglia verso l’alto con una forza piuttosto intensa, quelle nella regione rossa, invece, la attraggono verso il basso in maniera meno intensa, ma la regione rossa è molto più grande della viola, e quindi ci sono molte più particelle. In un certo senso, è come un tiro alla fune impari, in cui da una parte ci fosse una sola persona, ma molto abile, e dall’altra ci fossero molte persone ma poco abili nel gioco. Gli insiemi di particelle “rosse” e quelle “viola” attraggono la biglia in direzioni opposte, e si equivalgono, annullandosi: tanto le viola tirano la biglia verso l’alto, quanto le rosse la tirano verso il basso.

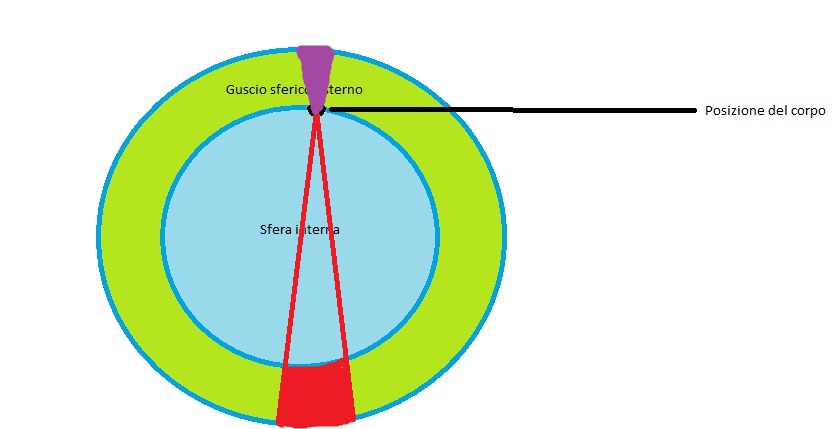
Otteneniamo quindi un risultato intuitivamente sorprendente: il guscio sferico non genera alcuna attrazione gravitazionale, e solo la massa interna della Terra la genera. Questo non significa che il guscio sferico non genera forza di gravità, ma che la forza di gravità che ogni suo punto genera è controbilanciata da altri punti nella parte opposta del guscio.

E quindi, la gravità diminuisce se andiamo sotto Terra?

Di conseguenza, questa è la risposta alla domanda iniziale: siccome solo la massa interna conta, più andiamo sotto Terra più l’attrazione gravitazionale è debole.

Se la biglia si trovasse al centro esatto della Terra, non subirebbe alcuna accelerazione gravitazionale, come se nel tiro alla fune gravitazionale, tutti i concorrenti tirassero con la stessa forza facendo rimanere immobile il punto centrale della corda. Di nuovo, non significa che al centro della Terra la gravità non ci sia, ma che la forza totale subita dal corpo è nulla perché attirato in ogni direzione in egual misura.

Il problema si potrebbe complicare a piacere, perché la Terra non è sferica e omogenea ma ha una forma e una composizione irregolare e quindi, in linea di principio, la legge di gravitazione universale non si potrebbe applicare come se tutta la massa fosse concentrata nel suo centro. Il guscio sferico non sarebbe effettivamente sferico, sarebbe un guscio bitorzoluto con i poli schiacciati e l’equatore allargato. Tutti questi fattori possono influenzare però solamente la modalità con cui la gravità diminuisce andando verso il centro della Terra, ma non il fatto stesso che la forza diminuisca.