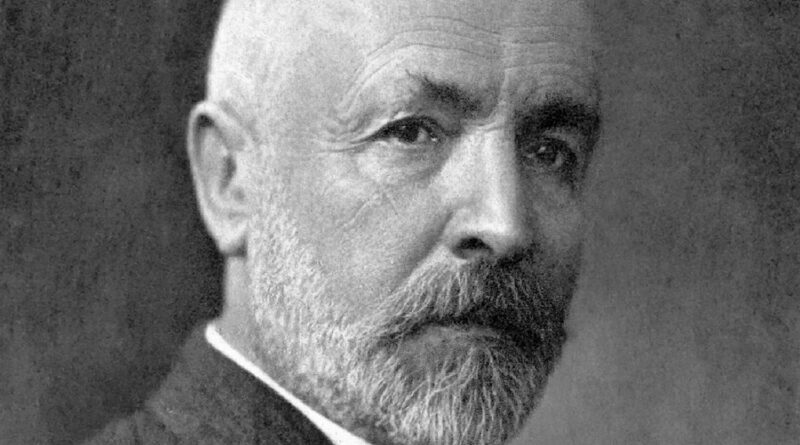L’Infinito di Cantor: breve storia dello scisma matematico

La nozione di infinito è sempre stata una questione spinosa nella storia della matematica. Georg Cantor è colui che ci ha dato una spinta definitiva per la sua comprensione in ambito matematico.

Alcune idee e tecniche, come quelle di calcolo, erano ben conosciute anche dalle culture egizie, babilonesi, indiane e cinesi ma la Matematica (quella con la M maiuscola) fatta di ricerca e di armonia nasce nella Grecia classica. Il personaggio che incarna questa rivoluzione della matematica è stato Euclide, che fondò ad Alessandria d’Egitto una delle Scuole più importanti che la storia ricordi, famosa per averci donato la più importante biblioteca del mondo antico.

Se nei secoli precedenti la matematica era usata come mero strumento di calcolo, la visione di Euclide era l’esatto opposto: credeva fermamente nella ricerca e disdegnava le applicazioni per fini puramente pratici. Per farci un’idea a riguardo si racconta che uno studente interrogò Euclide sull’utilità della matematica e quest’ultimo, dopo aver concluso la lezione, si rivolse a un suo schiavo dicendo “Dai una moneta a quel ragazzo, che cerca di ricavare un profitto da tutto ciò che impara”. Ovviamente il malcapitato studente venne immediatamente espulso.

Assiomi, teoremi, postulati: l’infinito

Euclide è inoltre riconosciuto per aver raccolto tutto lo scibile matematico allora conosciuto in 13 volumi, ribattezzati Elementi. L’opera tratta principalmente di geometria piana e di aritmetica ma la vera innovazione è nell’organizzazione del suo lavoro: vennero posti solidi punti di partenza, detti assiomi, da cui si potevano dedurre i teoremi. Le premesse da cui parte Euclide sono asserzioni da accettare al di là di ogni dubbio e che, quindi, non necessitano di dimostrazioni per essere confermate; difatti il termine assioma è una “affermazione degna di fede”.

Euclide introduce un’ulteriore novità usando il termine postulato, applicabile esclusivamente alla geometria. Dei cinque postulati ci vogliamo soffermare sul secondo ed il quinto. Il secondo recita:

Si può prolungare un segmento oltre due punti indefinitamente ^[1]

Il quinto, secondo la formulazione di Proclo, matematico e filosofo bizantino del 400 d.C., dice che:

Dati una retta r e un punto C fuori di r, esiste una sola retta passante per C e parallela a r, cioè priva di punti di intersezione con r ^[2]

In entrambi i casi, sia quando si postula la possibilità di prolungare un segmento indefinitamente sia quando si sostiene l’esistenza di rette che non si incontrano mai, si va a toccare un annoso e delicato problema: l’infinito.

Per sua stessa definizione, l’infinito è una “quantità” impossibile da classificare e misurare e entra in maniera quasi prepotente negli Elementi; una delle dimostrazioni più celebri di Euclide riguarda l’aritmetica e prova l’infinità dei numeri primi (libro IX degli Elementi). Questo è stato un primo tentativo di approccio a questo tema che ha diviso intere generazioni di matematici.

Ulteriori slanci verso l’infinito sono dovuti all’irrazionalità di  e i famosi paradossi di Zenone sulla divisibilità infinita o continuità.

Infinito potenziale e infinito attuale

Quando ci si approccia all’infinito è giusto però distinguere la sua forma potenziale da quella attuale.

La prima è da intendere come una grandezza variabile finita che continua a crescere portandosi oltre ogni limite finito (si prenda come esempio matematico la funzione 1/x), la seconda è da considerarsi come un singolo ente, una grandezza fissa, situata oltre tutte le grandezze finite. Per essere ancora più chiari, possiamo abbracciare l’idea che ci siano successioni senza fine di oggetti matematici e di “immaginare” porzioni comunque grandi di esse (infinito potenziale) ma non è possibile afferrare la totalità di questi elementi e identificarla singolarmente (infinito attuale).

Questa divisione non accontentava tutti i matematici, anzi trovava molti oppositori; uno dei più famosi fu l’illustre Kronecker che ribadiva incessantemente che gli interi positivi sono i soli numeri creati da Dio, come a indicare che già trattare con i numeri reali fosse qualcosa di sacrilego. Ma non fu solo Kronecker a scontrarsi contro questa idea, anche il matematico più famoso e importante dell’Ottocento (e dei nostri giorni), Carl Friedrich Gauss espose il suo disprezzo, nel 1831, per l’infinito attuale dicendo:

L’uso dell’infinito come qualcosa di definito… non è permesso in Matematica. L’infinito è solo un modo di dire, ed intende solo un limite cui certi rapporti possono approssimarsi vicino quanto si vogliono ^[3]

Gauss: il Re dei Matematici

La giungla degli infiniti

Altre menti autorevoli tentarono di avventurarsi nella giungla degli infiniti, avvertendone le insidie e i problemi, concludendo che forse era il caso di gettare la spugna e di passare oltre; uno di questi fu Galileo Galilei.

Egli pensava che un segmento era, ipoteticamente, composto da infinite parti, prive di estensioni, cogliendo così l’essenza dell’infinito attuale perché queste infinite parti ne erano una manifestazione; un ulteriore esempio può essere la circonferenza se considerata come un poligono regolare di infiniti lati. Ma ben presto si scontrò con delle difficoltà, che trattò nei Discorsi e dimostrazioni matematiche intorno a due nuove scienze nel 1638, presentando quelli che oggi sono conosciuti come Paradosso di Galileo e Paradosso della ruota.

Nel primo Galileo considera l’insieme dei numeri naturali e osserva che l’insieme infinito dei loro quadrati contiene tanti elementi quanti sono gli elementi dell’insieme di partenza dato che a ogni numero corrisponde in modo biunivoco il suo quadrato. L’insieme dei numeri naturali è così in corrispondenza biunivoca con un suo sottoinsieme proprio ma questo risultato è paradossale se si tiene conto del principio aristotelico-euclideo il tutto è maggiore della parte. Galileo commentò dicendo:

Io non veggo che ad altra decisione si possa venire che a dire infiniti essere tutti i numeri, infiniti i quadrati [..] ed, in ultima conclusione, gli attributi di eguale, maggiore e minore non aver luogo negl’infiniti ma solo nelle quantità terminate ^[4]

Senza entrare in dettaglio, questo principio è valido per gli insiemi finiti ma non per gli insiemi infiniti (come quello dei numeri naturali); il matematico tedesco Richard Dedekind usò questa caratteristica per precisare che in insieme è infinito quando, e soltanto quando, può essere posto in corrispondenza biunivoca con una sua parte propria.

Nel secondo paradosso si considerano invece due ruote concentriche e solidali; quando la più grande rotola e percorre un giro completo, anche la più piccola fa lo stesso ed entrambe percorrono due segmenti di eguale lunghezza. Ma come può una circonferenza più piccola essere “lunga” quanto una più grande? L’unica via di uscita era di ammettere una corrispondenza biunivoca tra la circonferenza piccola e quella grande, ma anche questo sembrava contraddire il principio sopra. Galileo fu obbligato a concludere:

“Queste son di quelle difficoltà che derivano dal discorrer che noi facciamo col nostro intelletto finito intorno all’infinito” ^[5]

L’albergo infinito di Hilbert

Le riflessioni fatte da Galileo col suo paradosso dei quadrati hanno dato lo spunto su come si possa “misurare” l’infinito: non si può semplicemente contare quanti elementi ci sono nei due insiemi, ma è possibile confrontarli e stabilire una corrispondenza biunivoca tra di essi. Questo ragionamento, ovviamente, è valido anche per altri tipo di insiemi infiniti dove si può stabilire, ove possibile, una corrispondenza biunivoca e dedurre se hanno lo stesso numero di elementi.

Una ulteriore argomentazione per analizzare il concetto di infinito va sotto il nome di Albergo di Hilbert, presentata dal grandissimo David Hilbert.

Supponiamo di avere un albergo composto da infinite stanze, tutte occupate da infiniti ospiti. Immagiamo che arrivi un forestiero che voglia una stanza per passare la notte, come può l’albergatore accontentarlo? Facendo spostare tutti gli ospiti nella camera successiva! Così l’ospite 0 va nella camera 1 (..) l’ospite N va nella camera N+1, liberando così una stanza. Quello che l’argomento di Hilbert sottolinea è che un insieme infinito può avere tanti elementi quanti un suo sottoinsieme proprio (come quello che si ottiene togliendo lo 0) e che la funzione successore, quella che trasforma N in N+1, è una corrispondenza biunivoca fra i naturali e i naturali maggiori di zero. Il ragionamento può essere iterato anche nel caso di infiniti nuovi ospiti.

L’infinito “a occhio” di Cantor

Chi diede però una decisiva svolta alla questione dell’infinito fu Georg Cantor, nella seconda metà dell’Ottocento.

Cantor, dotato da sempre di una fervida immaginazione, esplorò svariati insiemi infiniti. Osservò, ad esempio, che l’insieme dei numeri naturali N (0,1,2..) poteva essere valutato a occhio (una parola che può far storcere il naso a tutti i matematici del Mondo ma spero che mi perdonerete) come la metà dell’insieme dei numeri interi Z (-2,-1,0,1,2..); entrambi questi insiemi sono però infiniti (!) ma è possibile determinare una corrispondenza biunivoca che li collega. Basta osservare che i numeri naturali si suddividono a metà tra i pari e metà tra i dispari, “trasformare” gli interi negativi in quelli pari e quelli negativi nei dispari e si ha una bieezione tra N e Z.

Un altro analogo risultato fu quello che collega il quadrato (o anche il cubo) con il loro lato: entrambi hanno lo stesso “numero di punti”. Il teorema fu dimostrato e suscitò incredulità nel mondo matematico dato che il risultato sembra confondere enti geometrici di diversa dimensione, come curve, superfici e solidi, minando le basi della geometria. Lo stesso Cantor ne parlò in una lettera indirizzata all’amico, e matematico, Dedekind dicendo: “Lo vedo, ma non lo credo”.

C’è infinito e infinito

Le innumerevoli prove scovate da Cantor fanno presagire che tutti gli insiemi infiniti abbiano lo stesso numero di elementi, ma in realtà questo è un ragionamento sbagliato. Lo stesso Cantor nel 1874 dimostrò in maniera definitiva che non tutti gli infiniti sono uguali. Difatti il teorema affermava che non esiste una corrispondenza biunivoca tra l’insieme dei numeri naturali e quello dei numeri reali.

Cantor riuscì inoltre a generalizzare questo risultato provando che ci sono un’infinità di modi di essere infinto! Questa distinzione lo portò a classificare gli infiniti in base al loro “numero” di elementi, oltre a sviluppare un’apposita aritmetica, e lo condussero a formulare la Teoria degli Insiemi, oggi conosciuta con il nome di Teoria Ingenua degli Insiemi.

Cantor dimostrò, utilizzando questa nuova teoria, che dati due insiemi, se tra di essi esisteva una relazione di equivalenza (che determina una partizione di insiemi in classi), i due insiemi sono nella stessa classe se e solo se hanno lo stesso numero di elementi.

Le classi di equivalenza furono ribattezzate numeri cardinali. Tra questi numeri compaiono tutti i numeri naturali, che possono essere individuati con i cardinali degli insiemi infiniti, ma anche nuovi numeri infiniti, ad esempio (dove Alfef è la prima lettera dell’alfabeto ebraico) che Cantor usò per denominare il cardinale dei numeri naturali, a cui diedi il nome di numerabile; il cardinale dei numeri reali Cantor lo chiamò continuo.

La Congettura sull’infinito di Cantor

C’è un altro interessante argomento. Cantor dimostrò che l’insieme numerabile non ha tanti elementi come il continuo e si chiese se tra i due insieme infiniti N e R ci fossero altri infiniti intermedi. Presuppose di no, ma non riuscì a dimostrarlo e Hilbert inserì la questione nella lista di 23 problemi aperti della matematica presentanti al convengo del 1900 dei matematici a Parigi. La congettura di Cantor fu chiamata Ipotesi del Continuo e, ad oggi, la soluzione è solo parzialmente accettata.

Maneggiare l’infinito non è di certo un esercizio tranquillo. La questione presentava anche risvolti religiosi e Cantor, fervente credente e amante della teologia, distinse due infiniti attuali: uno che chiamò assoluto, che si applica solo a Dio e non è terrenamente accessibile, un altro che ribattezzò transfinito, che era l’infinito oggetto dei suoi studi.

Ma i tempi non erano dei migliori e già vari matematici illustri si erano opposti all’idea di infinito attuale (come Gauss nel 1831). Cantor dovette quindi affrontare la diffidenza dell’intera comunità scientifica: aspirava di ottenere l’ambito posto all’Università di Berlino, ma fu sempre ostacolato soprattutto dal matematico Kronecker. Quest’ultimo, facendo riferimento alle antiche concezioni pitagoriche, voleva che l’aritmetica e l’analisi venissero basate sui numeri interi. Affermava infatti che:

Il lavoro di Cantor sui numeri transfiniti e sulla Teoria degli Insiemi non è matematica, ma misticismo. Dio ha creato i numeri interi; tutto il resto è opera dell’uomo. ^[6]

I continui attacchi subiti portarono, nel 1884, Cantor ad avere il primo di una lunga serie di esaurimenti nervosi che si ripeterono con cadenza frequente per tutto il resto della sua vita e che lo portarono a morire in un ospedale psichiatrico nella città tedesca di Halle nel 1918.

Il suo lavoro venne successivamente capito e poi apprezzato. La sua tragedia personale trova però conforto nelle parole di alcuni grandi matematici del Novecento, tra cui Bertrand Russel, che nel 1910 scrisse:

La soluzione delle difficoltà che in passato circondavano l’infinito matematico è probabilmente la massima conquista che la nostra epoca ha da vantare ^[7]

E anche David Hilbert, uno dei matematici più influenti e importanti del XX secolo, si pronunciò in maniera superba nei suoi confronti:

La nuova aritmetica transfinita e la Teoria dei Cardinali sono una delle più belle creazioni del pensiero umano. Nessuno ci scaccerà mai dal paradiso che Cantor ha creato per noi ^[8]

Bibliografia:

• Stefano Leonesi, Carlo Toffalori – Matematica, miracoli e paradossi. Storie di cardinali da Cantor a Gödel. (Bruno Mondadori)
• Carl Boyer – Storia della Matematica (Oscar Saggi Mondadori, traduzione di Adriano Carugo)

Note:

• [1], [2], [3], [4], [5], [6], [8] Stefano Leonesi, Carlo Toffalor i- Matematica, miracoli e paradossi. Storie di cardinali da Cantor a Gödel (Bruno Mondadori)
• [4] Usato anche il Carl Boyer – Storia della Matematica (Oscar Saggi Mondadori, traduzione di Adriano Carugo)
• [7] Storie e protagonisti della matematica italiana. Per raccontare i 20 anni di “Lettera Matematica Pristem”.